对数函数的定义域及求解方法（探索对数函数的取值范围与限制）

对数函数是数学中重要的一类函数，广泛应用于各个领域。然而，对数函数的定义域及其求解方法却是让很多学生感到困惑的地方。本文将系统地介绍对数函数的定义域求解方法，并探讨其中的关键问题。

什么是对数函数

对数函数是一种用来描述指数运算的逆运算的函数。常见的对数函数包括自然对数函数（以e为底）和常用对数函数（以10为底）。在数学中，我们用log(x)表示以10为底的对数函数，ln(x)表示以e为底的自然对数函数。

对数函数的定义域概念

定义域是函数中自变量可以取值的范围。对于对数函数而言，定义域必须满足两个条件：自变量必须大于0，因为负数和0无法进行对数运算；底数不能等于1，因为任何数以1为底的对数都等于1。

常用对数函数的定义域求解方法

常用对数函数log(x)的定义域求解方法相对简单，只需考虑x的取值范围即可。由于常用对数函数的底数为10，因此定义域为x>0。

自然对数函数的定义域求解方法

自然对数函数ln(x)的定义域求解方法与常用对数函数类似，只需考虑x的取值范围即可。由于自然对数函数的底数为e，因此定义域为x>0。

对数函数中的特殊情况

当自变量取值为1时，对数函数会出现特殊情况。无论底数是多少，任何数以自己为底的对数都等于1。在求解对数函数的定义域时，需要排除自变量为1的情况。

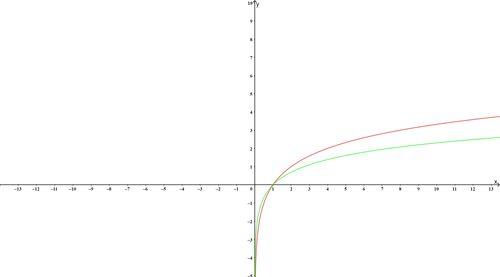
对数函数的图像特点

对数函数的图像特点是单调递增且无界的。无论底数是多少，对数函数始终是单调递增的，即随着自变量的增大，函数值也逐渐增大。同时，对数函数也是无界的，因为它可以取得任意大的正值。

对数函数在实际问题中的应用

对数函数广泛应用于实际问题中，例如在金融领域中用于计算复利、在物理学中用于描述衰减过程等。了解对数函数的定义域及其求解方法，有助于我们更好地理解和应用对数函数。

对数函数与指数函数的关系

对数函数与指数函数是密切相关的。对数函数是指数函数的逆运算，通过对数函数可以解决指数方程和指数不等式。对数函数的定义域的求解方法与指数函数的值域求解方法有一定的相似性。

对数函数的运算规律

对数函数具有一系列运算规律，例如对数的乘法法则、除法法则和幂次法则等。掌握这些运算规律可以简化对数函数的计算过程，并扩展对数函数的应用范围。

解决复杂对数方程的方法

有时候，我们需要解决复杂的对数方程。在这种情况下，我们可以通过转化为指数方程、利用对数函数的性质和运算规律等方法来求解。

对数函数在数值计算中的应用

对数函数在数值计算中有着重要的应用。通过使用对数函数，我们可以将大数字或小数字转化为较小或较大的整数，便于计算和比较。

对数函数与对数尺度

对数函数的定义域及其求解方法与对数尺度有着密切关系。对数尺度是一种用于处理非常大或非常小的数值的测量尺度，通过对数函数可以方便地进行对数尺度的计算和比较。

对数函数的局限性和注意事项

尽管对数函数在很多领域中有着重要的应用，但我们也需要注意到对数函数的一些局限性。例如，在计算机中进行对数运算时需要考虑精度问题，以免产生误差。

举例说明对数函数的定义域求解

通过几个具体的例子，我们可以更好地理解和应用对数函数的定义域求解方法。这些例子将帮助读者更好地掌握对数函数的相关概念和技巧。

对数函数是一种重要的数学函数，了解其定义域及其求解方法对于深入理解和应用对数函数至关重要。本文系统介绍了对数函数的定义域求解方法，并讨论了与之相关的关键问题，希望能为读者提供帮助。